Desafíos geométricos (Segunda parte)

La presente propuesta expone una secuencia de desafíos que vienen siendo llevados a la práctica con la intención de promover en territorio la enseñanza de la Matemática en forma lúdica, dinámica, exploratoria, reflexiva, crítica y colaborativa, optimizando todos los insumos con que cuenta el docente del siglo XXI en Uruguay.

Para entender cabalmente esta secuencia se sugiere ver la propuesta didáctica ya publicada (antecedentes) aquí

Cuarto desafío: Luego de lo experimentado en el desafío anterior (el tercero), debatir en clase (en plenario o en pequeños grupos) acerca de la validez y alcance de lo que puede leerse en la pestaña “Consultar” que brinda la PAM, en la actividad propuesta para 4° grado de Primaria, apartado Geometría, ítem N° 8 (construir rectángulos), Actividad 1, en donde se plantea una situación similar al desafío tres.

Consigna: Reúnete con un compañero, respondan la Actividad 1 y luego revisen lo que ofrece Betty en la pestaña “Consultar”, en la página 2.

• ¿Están de acuerdo con lo que allí se explica?
• ¿Agregarían algunas puntualizaciones?
• En caso afirmativo: ¿cuáles?
• En caso negativo: ¿por qué?

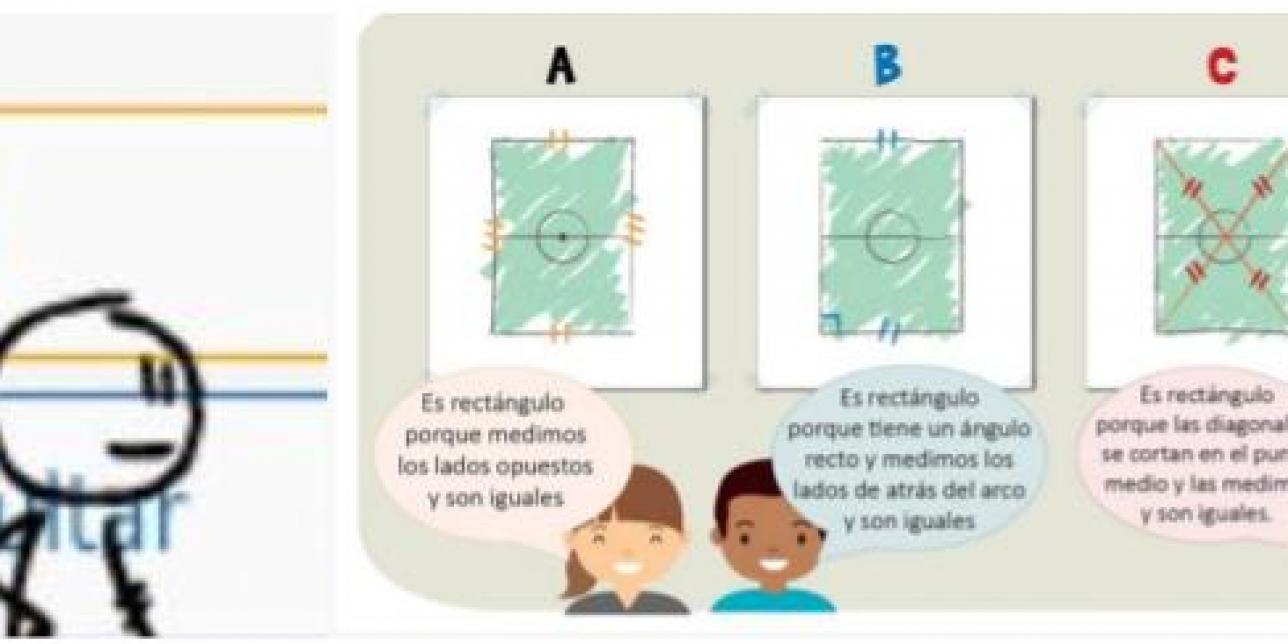
Quinto desafío: Atendiendo a las propiedades de las figuras, en las pruebas formativas del SEA para 6° grado, se presentó esta actividad en donde implícitamente se le pide al estudiante que reconozca cuáles de las apreciaciones de los niños responde a características necesarias y suficientes para determinar un rectángulo.

• A
• B
• C
• D

Aportes para la reflexión docente:

Esta actividad tiene como principal riqueza la posibilidad de habilitar debates  acerca de la validez de cada uno de los argumentos dados por los niños del ítem. Analizar cuál de esos argumentos es la condición de suficiencia para definir al rectángulo torna a la propuesta en un valioso insumo para profundizar en el conocimiento y dominio de las propiedades de la figura geométrica en cuestión.

Dado que la respuesta correcta es la C, el maestro puede hacer notar la particularidad del cuadrado (cuadrilátero regular) como rectángulo especial.

Extender estas reflexiones a otras figuras del plano hará que los niños construyan conceptos cada vez más sólidos en torno a cada una de ellas. Experimentar si las observaciones planteadas por los niños resisten la prueba del arrastre en Geogebra la potenciaría aún más. El trabajo con el error siempre es fuente de aprendizajes significativos.

Para realizar las prácticas en línea pueden pulsar aquí.