Contenido - 5° grado: Relaciones entre perímetro y área.
Propósito:
Promover la exploración y comparación entre los perímetros y las áreas de las distintas figuras geométricas representadas en el Tangram para que los estudiantes arriben a la conclusión de que las figuras (o las composiciones de figuras) a pesar de tener igual área pueden tener diferente perímetro. Perímetro y área son magnitudes independientes.
Consignas para el estudiante:
Propuesta 1:
|
Jacinta tiene un Tangram con piezas iguales a las de este modelo:
|
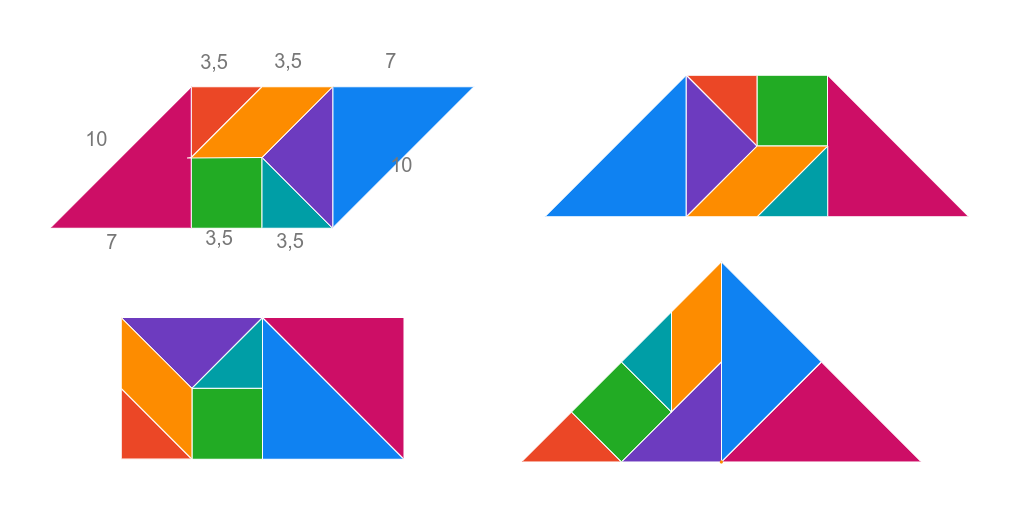
Construyó cuatro composiciones de figuras usando siempre sus siete piezas. Las fotografió y las compartió en el aula virtual de su curso. Al verlas concluyó:
|
||||
|
|||||
Propuesta 2:
Para esta investigación te ofrecemos dos modelos de plantillas para descargar y recortar.
Con uno de esos modelos de Tangram podrás reproducir las construcciones que hizo Jacinta.
Sabiendo que las piezas son las mismas en cada construcción, ¿cuáles de las siguientes afirmaciones son correctas?
- Todas las construcciones tienen igual área.
- Todas las construcciones tienen igual perímetro.
- Las construcciones tienen igual área pero algunas distinto perímetro.
- Las construcciones tienen distinta área y distinto perímetro.
Propuesta 3:
Ramiro está seguro que todas las figuras que construyó Jacinta tienen igual área porque fueron compuestas por la misma cantidad y tipo de piezas. Pero sospecha que no pasa lo mismo con el perímetro.
Para investigar si su hipótesis es verdadera hizo esto:
|
1) Colocó las piezas de su Tangram sobre papel cuadriculado y compuso todas las figuras de Jacinta, una en cada hoja:  |
2) Marcó el lugar de cada vértice sobre el papel: 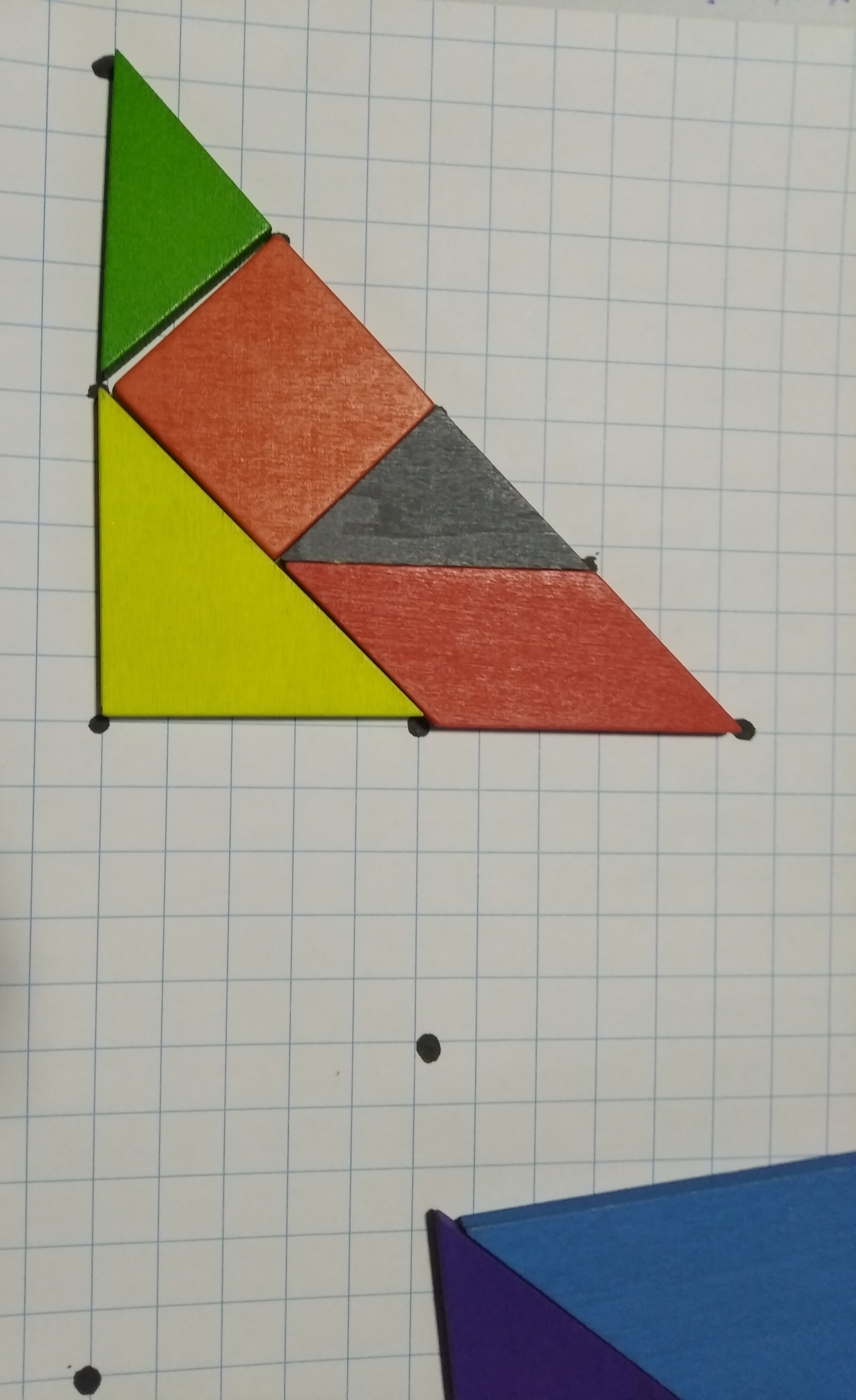 |
|
3) Trazó el contorno o silueta de la construcción con línea entera, y con línea punteada, los lados de las figuras que quedaron en el interior. 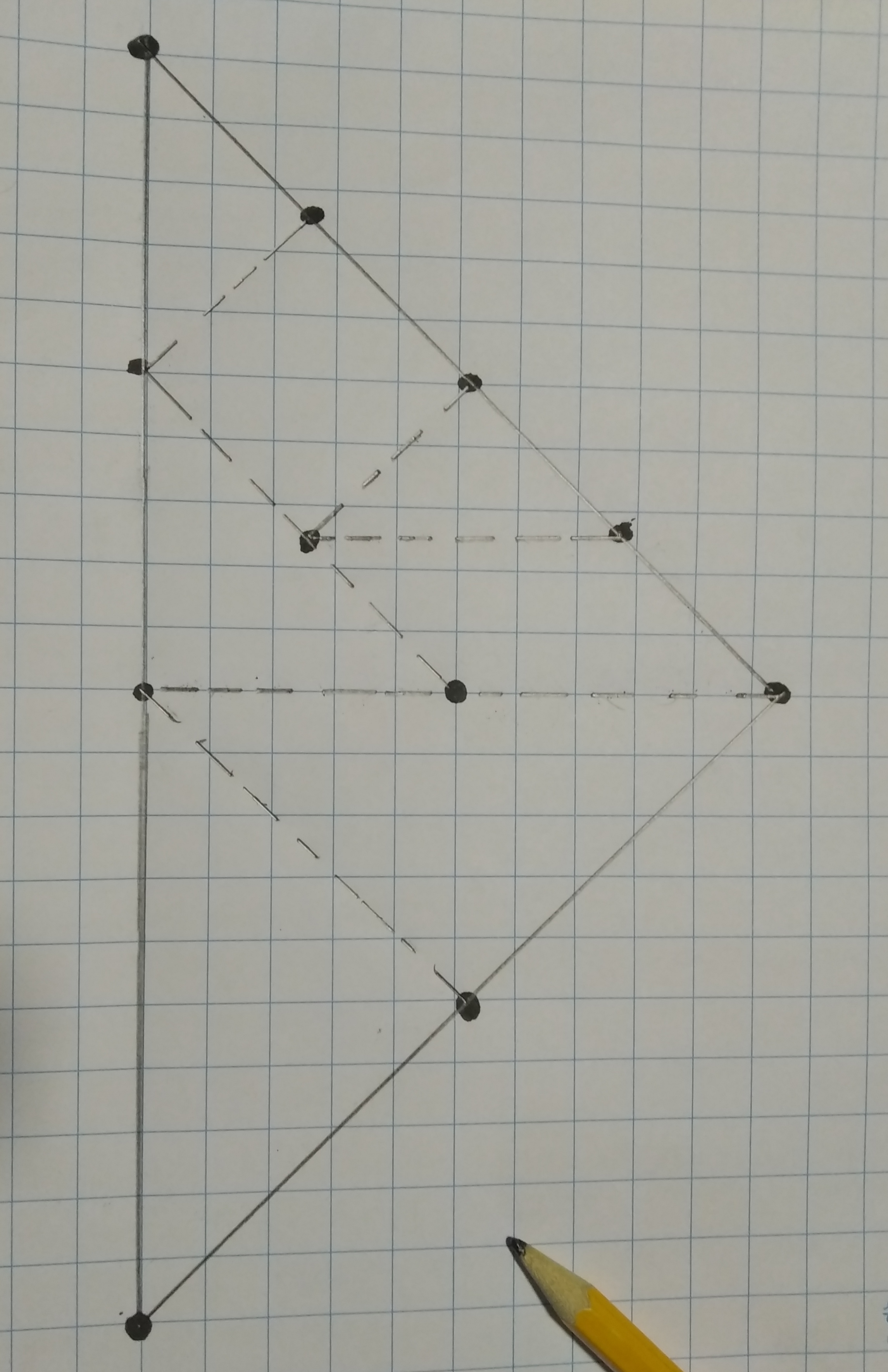
|
4) Midió y comparó las longitudes de todos los lados de las piezas que componen el contorno de cada construcción. Consideró al largo del lado de cada cuadradito de la cuadrícula de fondo como unidad de medida (1cm) para medir los lados de las figuras, y la regla centimetrada en los casos que fue necesario.
|
|
Estas fueron las medidas que tomó para el caso de la construcción 4: 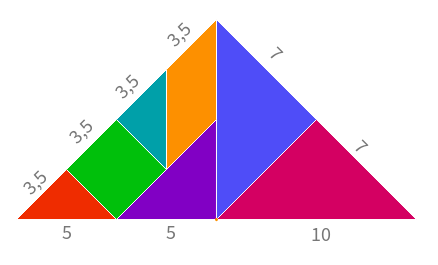 |
|
Ramiro observó lo siguiente:
- Los triángulos son rectángulos isósceles, por lo tanto uno de sus lados (hipotenusa) es de mayor longitud que los lados iguales. Entonces, si ese lado largo queda en el interior de la figura que compuso Jacinta no es lo mismo que si queda como lado de la composición.
- Con el cuadrado, en cambio, como se trata de un polígono regular, sus lados siempre sumarán la misma longitud en la medida total del contorno de las figuras (su perímetro).
- ¿Cuánto mide el perímetro de la construcción triangular que se ve en el modelo de Ramiro?
- Teniendo en cuenta las medidas escritas por Ramiro en esa imagen, ¿cuál es el perímetro de las otras tres construcciones?
- ¿Cuáles son las construcciones que Ramiro descubrió que tienen igual perímetro?
- Ahora volvamos al tablero cuadrado del Tangram (con las mismas 7 piezas):
- a) ¿qué puedes decir de su perímetro? Es mayor que el de la composición...; es menor que el de la composición...; es igual que el de la composición...
- b) ¿Y de su área?
Propuesta 4:
Ramiro siguió explorando las áreas de las piezas del Tangram y descubrió estas relaciones:
- El área del triángulo azul es el doble del área del triángulo violeta.
- El área del cuadrado es el doble del triángulo rojo.
- El área de los dos triángulos más grandes es igual al área de todas las otras piezas juntas.
- El área del cuadrado y el área del paralelogramo tipo, ¿son iguales?
¿Qué otras relaciones descubres tú?
Propuesta 5:
Ya exploraste junto a Jacinta y Ramiro las relaciones entre perímetro y área de todas sus composiciones con el Tangram. Estás en condiciones de clasificarlas según estos criterios:
- Construcciones que tienen igual área que el Tablero Tangram:....................................................................
- Construcciones que tienen mayor perímetro que el Tablero del Tangram pero menor perímetro que la Construcción 2:.......................................................................
- Construcciones que tienen mayor perímetro que la Construcción 1:..........................................................
Propuesta 6 - Desafío final:
 Empleando las siete piezas del mismo Tangram de Jacinta y Ramiro, ¿lograrás construir una composición que tenga perímetro mayor a las que ellos fabricaron? Si lo logras, tómale una fotografía y envíala a esta dirección de correo: consultaparaportales@gmail.com
Empleando las siete piezas del mismo Tangram de Jacinta y Ramiro, ¿lograrás construir una composición que tenga perímetro mayor a las que ellos fabricaron? Si lo logras, tómale una fotografía y envíala a esta dirección de correo: consultaparaportales@gmail.com
 Ante cualquier idea, consulta, propuesta o sugerencia pueden comunicarse con el equipo de Matemática uniéndose al Grupo "S.O.S. Geometría" en CREA con este código de acceso: HC3KR-4ZMPR.
Ante cualquier idea, consulta, propuesta o sugerencia pueden comunicarse con el equipo de Matemática uniéndose al Grupo "S.O.S. Geometría" en CREA con este código de acceso: HC3KR-4ZMPR.