Propuesta para segundo año - El resto de la división

Análisis de una propuesta de aula realizada en un grupo de segundo año escolar y de algunas de las resoluciones de los niños.

Tipo de actividad:

Trabajo Individual.

Propósitos:

Contribuir a la compresión del significado de la operación división, vinculando los términos relacionados a la misma.

Criterios de evaluación:

No se determinan para esta actividad.

Contenido:

Relación entre los términos de la división.

Actividades:

La propuesta

El problema se le presenta a un grupo de niños de segundo año escolar por escrito, como una tarea a realizar en forma individual.
El algoritmo convencional de la división no se había introducido aún en el aula.

La consigna

Después de un cumpleaños, una mamá repartió a sus tres hijos unos caramelos que habían quedado. Le dio la misma cantidad de caramelos a cada hijo y le sobró uno que se lo comió ella. ¿Cuántos caramelos habrían quedado?

El problema plantea el caso de un reparto que podría resolverse, dado que el mismo es equitativo, mediante el empleo de una división en la que se consideren como dividendos los números que se presentan como opciones, como divisor el 3 y contemplando que el resto deberá ser 1 para determinar el dividendo que resulte adecuado (cantidad de caramelos que quedaron del cumpleaños).

A continuación se presentan algunas de las resoluciones de los niños al problema presentado:

Maximiliano

En este caso, se observa que si bien su respuesta es la adecuada, el niño parece realizar un reparto entre cuatro (que se pone en evidencia a través de una suma) y no entre los tres hermanos que indica el problema. Cabría preguntarse entonces qué significan para el niño cada uno de los números tres empleados como sumandos. Para despejar la duda, se cuestiona al niño:

Maestra: ¿Para qué hiciste esta cuenta?
Alumno: Para ver los caramelos.

M: ¿Cuántos caramelos habían quedado?
A: Trece

M:¿Qué son estos "tres" que aparecen en la cuenta?
A: Los tres hermanos.

M:¿Todos estos tres son los tres hermanos? ¿Cuántos hijos tenía la mamá?
A: Eran tres hermanos.

M: ¿Y este "uno" que está acá? - señalando el 1 de la cuenta
A: El caramelo que comió la mamá. Los caramelos son estos -señalando los números tres- de los hermanos.

M: ¿Con cuántos caramelos se quedó cada hermano?
A: Con uno, dos, tres y cuatro - cuenta los números tres que escribió en la operación - porque la mamá se los dio uno y uno y uno a los hijos y otra vez uno y uno y uno y les dio cuatro.

Por lo que se aprecia a partir de la entrevista, Maximiliano se representó la situación y se hizo la imagen de la mamá repartiendo los caramelos uno por uno, luego de repartir un caramelo a cada uno de los tres hijos llevaba tres caramelos repartidos y registró un número tres, repartió otro caramelo a cada hijo y anotó otro tres. Así llegó a repartir los doce caramelos entregando cuatro a cada hijo, que sumados al uno que aparece debajo, corresponden a los trece caramelos que habían quedado.

Cabría preguntarse, aunque no se indagó al niño al respecto, cómo fue descartando el resto de las opciones hasta quedarse con el 13 como respuesta.

Katherine

La niña analiza uno a uno los posibles casos, es decir, considera todas las cantidades de caramelos posibles, realiza un reparto equitativo para los tres hermanos, observando si le sobran o no caramelos, eligiendo por tanto aquel caso en el cual el resto es uno.

Michael

Michael explica cómo encontró que se trataba de trece caramelos y argumenta sobre la razón por la cual no podrían ser dieciocho. Realiza un reparto equitativo entre los hermanos y se fija en el caramelo que debe agregar para que coma la mamá.

Tal vez necesitó detallar este otro caso en particular (dieciocho) porque era mayor cantidad de caramelos y lo pensó como una posibilidad, ya que no argumenta acerca del resto de las opciones.

Jonathan

Explicita el razonamiento seguido para encontrar el dividendo a través de la suma reiterada del número cuatro (correspondiente a la cantidad de caramelos que recibe cada niño y cociente en el caso de la división). Para asegurar que las otras opciones no son válidas, fundamenta a través del resto de la división "si no, no le sobra uno para la mamá".

No se observa en la explicación de Jonathan el modo en que obtuvo el cuatro como número de caramelos para cada hermano, o sea, como cociente.

Carla

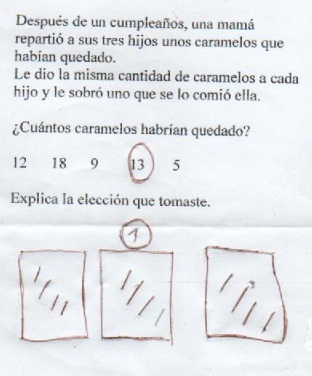
El caso de Carla que, aparentemente podría considerarse como menos avanzado dado que realiza marcas en la hoja en lugar de trabajar con los números o brindar explicaciones por escrito (como lo hacen algunos de sus compañeros), resulta muy interesante de analizar.

Ella indica en las opciones que el número de caramelos es 13 y como explicación aparece lo que puede observarse en la imagen. ¿Cómo interpretarla? Desde la mirada del docente podría observarse que aparecen presentes los elementos de la división, los 13 caramelos o dividendo considerando las 12 rayitas más el "1" encerrado más arriba que correspondería al resto, los 3 niños o divisor representados por los tres cuadros, el 4 como cociente de la división formado por las rayitas.

¿Cuál fue el proceso seguido por la niña para realizar este registro? Para estar seguros del mismo se le pregunta a la niña sobre el significado de su registro.

Maestra:¿Cuántos caramelos habían quedado del cumpleaños?
Alumna: trece.

M:¿Qué es esto que pusiste acá? (señalando el registro de la niña).
A: La mamá comió uno así que lo puse acá y en estos cuadrados es los caramelos de los niños, dos tres y cuatro (indicando en cada caso la primera rayita de cada cuadro), cinco acá (señalando la segunda rayita del primer cuadro). No sirve el cinco porque no le da igual a todos y después seguí poniendo los caramelos.

M: ¿Y no podían ser nueve caramelos?
Carla comienza a contar nuevamente desde el "1" de la mamá hasta llegar a nueve.
A: no porque le da menos caramelos a este niño, le da dos y a los otros tres. Es trece porque el doce lo puedo repartir justo para los tres hermanos.

Lo que resulta interesante del análisis de este modo de resolver el problema y de los argumentos que brinda la niña, es que al aislar de entrada el resto (el caramelo que come la madre), Carla pasa a trabajar con una división exacta. Mientras que el resto de los niños realizaba el reparto y observaba el resto para corroborar si era uno, Carla quita el resto para repartir lo que queda entre los tres hermanos, para el caso de esta situación, busca si el número anterior a los propuestos como posibles, es múltiplo de tres.

El análisis de las resoluciones de los niños nos permite conocer lo que ellos saben sobre el contenido matemático que se está trabajando, y por lo tanto, pensar cómo podemos hacer para que sigan avanzando. Brindando oportunidades diferentes para trabajar con la división y con sus diferentes significados, presentando situaciones en las cuales no siempre se pregunte por el cociente y se pretenda siempre el empleo del algoritmo convencional, diseñando problemas que apunten a establecer relaciones (tanto entre los elementos de la división como con otras operaciones) se estará aportando a la construcción del concepto de la división.