Recordemos la definición de seno, coseno y tangente.

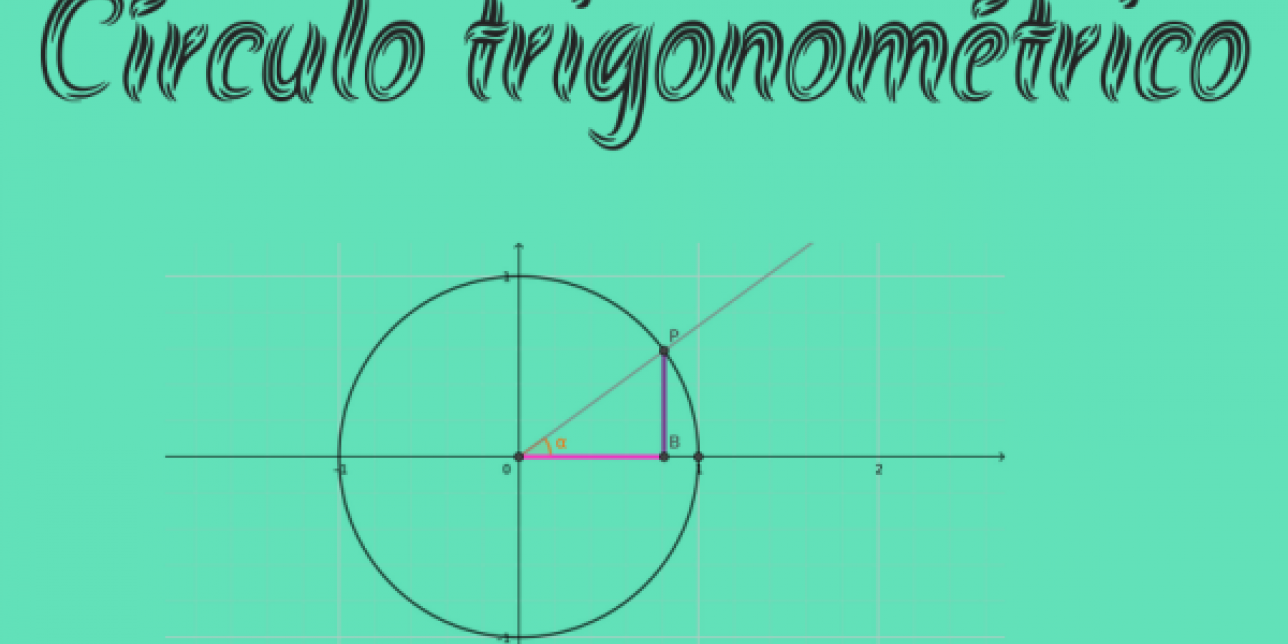
El siguiente es el círculo trigonométrico. Observa que está centrado en el origen de coordenadas y su radio es igual a 1.

Sabiendo esto y analizando el triángulo OBP :

• Plantea seno y coseno  del ángulo α, en función de la medida de los lados del mismo.

• ¿Se relacionan el seno y el coseno con las coordenadas del punto P?
• Activa la casilla "coordenadas de P" y verifica tu afirmación.

Analiza OBP nuevamente.

• ¿Es posible aplicar Pitágoras en él? Explica.
• En caso afirmativo escribe la relación encontrada usando el seno y el coseno de alfa.
  
   
• Plantea, en función de la medida de los lados de OBP, la tangente del ángulo α.
• ¿Puedes relacionarla con el seno y el coseno de α? Explica.

Si mueves el deslizador α cambiarás la amplitud del ángulo y podrás colocar a P en cada uno de los cuadrantes determinados por el sistema de ejes cartesianos.

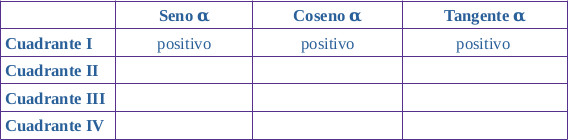
Recordando la relación existente entre las coordenadas de P, el coseno y el seno de α, indica el signo de los mismos en cada cuadrante.

Luego, teniendo en cuenta la relación entre seno, coseno y tangente de α, deduce el signo de la tangente de α en cada cuadrante.