Alturas de un triángulo

Alturas de un triángulo

Definición : Se denomina altura de un triángulo al segmento de perpendicular trazado desde un vértice al lado opuesto.

Si mueves los vértices del triángulo podrás ver que la altura puede ser interior, exterior o ser un lado del triángulo, dependiendo si el triángulo tiene todos los ángulos agudos, tiene un ángulo obtuso o tiene un ángulo recto.

Como los triángulos tienen tres vértices y tres lados entonces tendremos tres alturas.

Propiedad :
Las rectas que contienen a las alturas se cortan en un punto llamado Ortocentro.

Veamos como justificar dicha propiedad.

Usemos el siguiente applet para ayudarnos.

Primero consideraremos un triangulo auxiliar trazando rectas paralelas a los lados del triángulo ABC por cada uno de los vértices opuestos. Haz clic en la casilla triángulo auxiliar para visualizarlo.

Puedes ver entonces el triángulo EFD cuyos lados son paralelos a los del ABC y pasan por los vértices del mismo.

Al trazar este triángulo podemos ver tres nuevos triángulos que están en amarillo en la figura. (FAC , DAB, BCE)

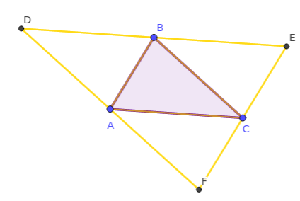
Se puede probar que estos tres triángulos son iguales al ABC. Nos alcanza con analizar que tienen un lado común con él y como las rectas son paralelas puedo probar por ángulos alternos internos que cada uno de ellos tiene dos ángulos iguales a los del ABC.

Observemos para uno de ellos (DBA y ABC):
Por ejemplo las rectas DB y AC son paralelas entonces por la propiedad de los ángulos alternos internos entre ellas, los ángulos DBA y BAC son iguales. Las rectas DA y BC son paralelas entonces por alternos internos entre ellas los ángulos DAB y ABC son iguales. Además esos dos triángulos tienen el lado AB en común así que se puede concluir que los triángulos son iguales.

De la misma manera justificamos la igualdad de los tres triángulos que están de color amarillo y el ABC.

Como los triángulos son iguales podemos concluir entonces las siguientes igualdades de segmentos: DB=BE, DA=AF y EC=CF, por lo tanto los puntos A, B y C  son los puntos medios de los lados del triángulo DEF.

Tracemos ahora las mediatrices de los lados del EDF y con ellas aparecerá determinado el circuncentro de dicho triángulo. Haz clic en la casilla circuncetro de DEF para visualizarlo.

Las mediatrices  de los lados DF, DE y FE  pasan por A, B  y C, porque son los puntos medios de dichos segmentos. Además son perpendiculares a las rectas BC, AC y AB, porque, por ser mediatrices, son perpendiculares a las rectas DF, DE Y EF y estas a su vez, son paralelas a BC, AC y AB por la construcción.

Por lo tanto, las mediatrices de los lados del triángulo DEF contienen a las alturas del triángulo ABC. Haz clic en la casilla Ortocentro de ABC.

Como las mediatrices de un triángulo concurren en el circuncentro y las alturas del triangulo ABC están incluidas en la mediatrices del EFD podemos concluir que las rectas que contienen las alturas de un triángulo son concurrentes en el punto que llamamos Ortocentro.

El circuncentro del DEF coincide con el ortocentro del ABC.

Bibliografía:

Borbonet, M., Burgos,B., Martínez, A. y Ravaioli, N. (2007). Matemática2, Grupo Botadá. Montevideo: Fin de Siglo