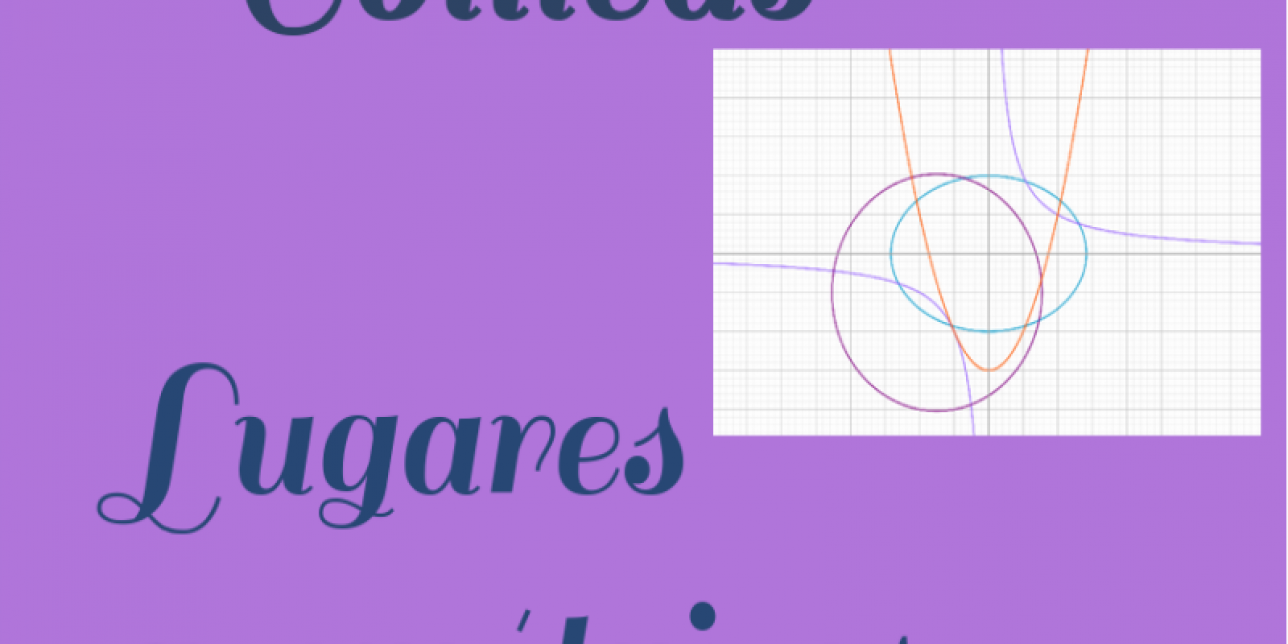
Las cónicas como lugares geométricos
Si investigas acerca de las cónicas encontrarás dos formas de definirlas.
La primera hace referencia a que son las curvas que se obtienen al cortar una superficie cónica con un plano y la segunda, referida a que son Lugares geométricos (conjuntos de puntos que cumplen una propiedad).
Te presentamos aquí una forma de definir las cónicas como lugares geométricos pero algo diferente de los que puedes encontrar en la mayoría de los textos, ya que solo partiremos de un punto F, una recta d y una razón k.
Utilizando el siguiente applet realiza la actividad:
1. Moviendo el deslizador a fija la recta d y el punto F en una posición.
2. Moviendo el deslizador k fíjalo en un número mayor que 1.
3. Mueve ahora el punto "mover" por toda la pantalla y observa que cónica está describiendo dicho punto.
4. Haz clic sobre la casilla P y podrás ver qué trazados se han hecho para encontrar los puntos P.
4. Refresca la pantalla con las dos flechas circulares que encuentras en las esquina superior derecha.
*Repite la actividad para otros valores de k.
*Lo mismo pero tomando K menor que 1 y luego igual a 1
Analicemos que es lo que estamos observando:
Los puntos P los obtienes a partir de la intersección de circunferencias de centro el punto F y rectas paralelas a la recta d.
¿Cómo se conectan estas dos figuras con el número k que seleccionas en este applet?
El radio de la circunferencia divido la distancias entre la recta f y la d nos da el valor de k elegido. Por lo que resulta que la distancia de cada P encontrado al punto F, dividido la distancia de dicho P la recta d es k (d(P,F)/d(P,d) = k)
| Por lo tanto podríamos decir que una cónica es el lugar geométrico de los puntos de un plano cuya razón de distancia a un punto F y a una recta d es una constante k |
Como has podido observar en el applet, según el valor de k elegido sea mayor, menor o igual a 1, la cónica obtenida será una hipérbola, elipse o parábola respectivamente.
Clasificación Curricular
Imagen descriptiva: Sin título. Autor: Sylvia Borbonet. Licencia Creative Commons Atribución 4.0 Internacional.
Applet: Borbonet, S. (2019). Lugares Geométricos. [Applet]. Recuperado de: https://www.geogebra.org/m/eggbtpgd